A Sequential circuit is a combinational logic circuit that consists of inputs variable, logic gates (Computational circuit), and output variable. Sequential circuit produces an output based on current input and previous input variables.

Types of Sequential Circuits –

1. synchronous sequential circuit - These circuit uses clock signal and level inputs (or pulsed) (with restrictions on pulse width and circuit propagation). The output pulse is the same duration as the clock pulse for the clocked sequential circuits. Since they wait for the next clock pulse to arrive to perform the next operation, so these circuits are bit slower compared to asynchronous. Level output changes state at the start of an input pulse and remains in that until the next input or clock pulse.

   

2. Asynchronous sequential circuit - These circuit do not use a clock signal but uses the pulses of the inputs. These circuits are faster than synchronous sequential circuits because there is clock pulse and change their state immediately when there is a change in the input signal. We use asynchronous sequential circuits when speed of operation is important and independent of internal clock pulse.

   

Flip-flop is a circuit that maintains a state until directed by input to change the state. A basic flip-flop can be constructed using four-NAND or four-NOR gates.

Types of flip-flops:

1. RS Flip Flop
2. JK Flip Flop
3. D Flip Flop
4. T Flip Flop

Logic diagrams and truth tables -

• 1 S-R Flip Flop :
  
  

  Characteristics Table:

  S	R	Qn	Q(n+1)
  0	0	0	0
  0	0	1	1
  0	1	0	0
  0	1	1	0
  1	0	0	1
  1	0	1	1
  1	1	Invalid
  1	1	Invalid

  Excitation Table:

  Qn	Q(n+1)	S	R
  0	0	0	x
  0	0	1	0
  1	0	0	1
  1	1	x	0

• 2 J-K Flip Flop:
  
  

  Characteristics Table:

  J	K	Qn	Q(n+1)
  0	0	0	0
  0	0	1	1
  0	1	0	0
  0	1	1	0
  1	0	0	1
  1	0	1	1
  1	1	0	1
  1	1	1	0

  Excitation Table:

  Qn	Q(n+1)	J	K
  0	0	0	x
  0	1	1	x
  1	0	x	1
  1	1	x	0

• 3 D Flip Flop :
  
  

  Characteristics Table:

  D	Qn	Q(n+1)
  0	0	0
  0	1	0
  1	0	1
  1	1	1

  Excitation Table:

  Qn	Q(n+1)	D
  0	0	0
  0	0	1
  1	0	0
  1	1	1

• 4 T Flip Flop :
  
  

  Characteristics Table:

  T	Qn	Q(n+1)
  0	0	0
  0	1	1
  1	0	1
  1	1	0

  Excitation Table:

  Qn	Q(n+1)	T
  0	0	0
  0	0	1
  1	0	1
  1	1	0

Steps to solve a problem:

1: Draw the state diagram from the problem statement or from the given state table.

Example: Serial Adder.
The functioning of serial adder can be depicted by the following state diagram. X1 and X2 are inputs, A and B are states representing carry.

2: Draw the state table. If there is any redundant state then reduce the state table.

3: Select state assignment i.e. assign binary numbers to the states according to total number states. Also decide the memory element (flip-flops) for the circuit.
A -> 0
B -> 1

4: Replace the assignments in the state table to obtain Transition table:

5: Separate the output table from the transition table.

Z = x1x’2y+x’1x2y’+x1x2y+x1x’2y’

6: Excitation table for the flip-flop is obtained from the transition table using the output of flip-flop.
Excitation table for D flip-flop:

D = x1x2 + x1y + x2y

7: Draw the circuit diagram using gates and flip-flops.

In the RTL Design methodology different types of registers such as Counters, Shift Register, SIPO (Serial In Parallel Out), PISO (Parallel In Serial Out) are used as the basic building blocks for any Sequential Logic Circuits.

Example -

Step to design Up Counter (for 0-3):

1. Step 1: the 1st step we draw a State Diagram representing the above sequential circuit. The State Diagram representing the above counter is shown below:


2. Step 2: In the next step we derive the State Table from the above given State Diagram
   The State Table is as given below:

   Present State Q(n)	Next State Q(n+1)	Output
   00	01	01
   01	10	10
   10	11	11
   11	00	00

3. Step 3: In the third step we need to choose the type of flip flop we will be using to store the state of the circuit, for simplicity, we will be considering the Positive Edge Triggered D-type Flip-Flop.We also need to determine the number of Flip-Flops required to represent the internal state of the circuit. The general formula for the number of Flip-Flops required:

   Then we need to note down the Excitation Table for chosen Flip-Flop. The Excitation Table for the D-type Flip-Flop is shown below:

   Present State Q(n)	Next State Q(n+1)	D
   X	0	0
   X	1	1

4. Step 4: In this step we combine the State Table from the 2nd step with the excitation table of the previous step as follows:

   QA(n)	QB(n)	QA(n+1)	QB(n+1)	DA	DB
   0	0	0	1	0	1
   0	1	1	0	1	0
   1	0	1	1	1	1
   1	1	0	0	0	0

5. Step 5:Next, from the above table we try to express D_A, D_B as boolean functions of Q_A(n), Q_B(n). In this case the expression for both D_A, D_B are trivial.

   D_A = Q_A ⊕ Q_B   D_B = Q'_B

   The Final Sequential Circuit is shown below:

   

A Counter is a device which stores (and sometimes displays) the number of times a particular event or process has occurred, often in relationship to a clock signal.

Counter Classification

1. Asynchronous counter

   In asynchronous counter we don’t use universal clock, only first flip flop is driven by main clock and the clock input of rest of the following flip flop is driven by output of previous flip flops. We can understand it by following diagram-

   

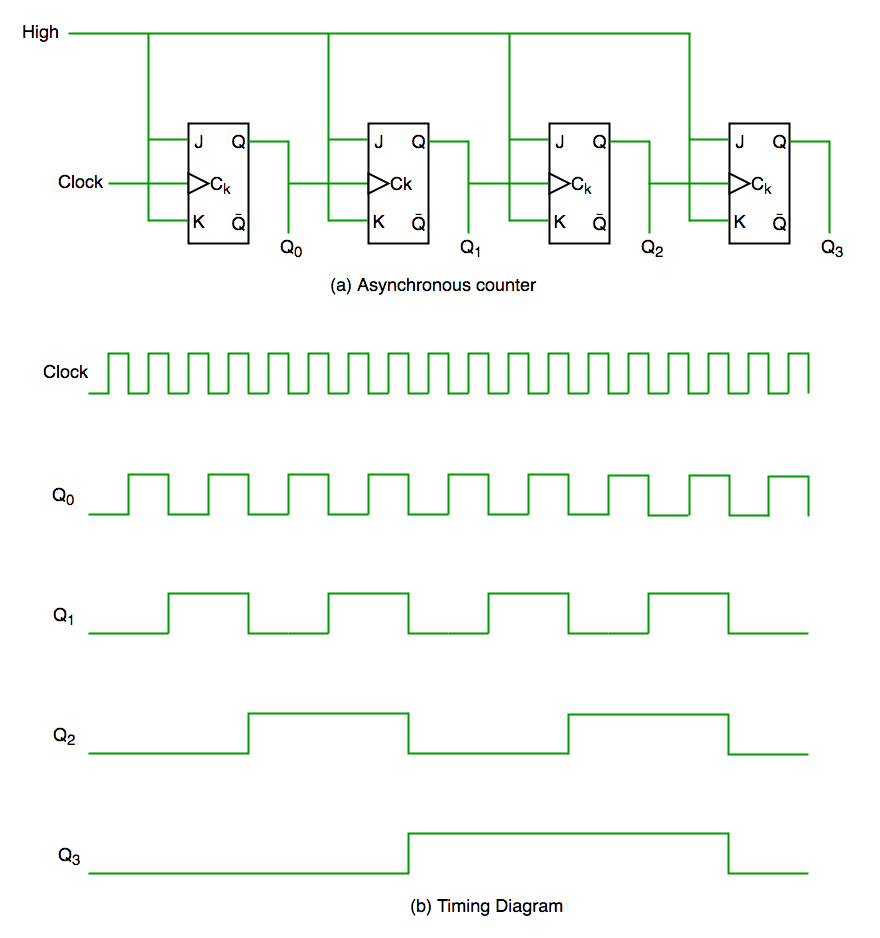
2. Synchronous counter

   Unlike the asynchronous counter, synchronous counter has one global clock which drives each flip flop so output changes in parallel. The one advantage of synchronous counter over asynchronous counter is, it can operate on higher frequency than asynchronous counter as it does not have cumulative delay because of same clock is given to each flip flop.

   

---

Design counter for given sequence -

Problem Design synchronous counter for sequence: 0 → 1 → 3 → 4 → 5 → 7 → 0, using T flip-flop.

Step-1:For given sequence, state transition diagram as following below:

Step-2:State transition table for given sequence:

Q3	Q2	Q1	Q3(t+1)	Q2(t+1)	Q1(t+1)
0	0	0	0	0	1
0	0	1	0	1	1
0	1	1	1	0	0
1	0	0	1	0	1
1	0	1	1	1	1
1	1	1	0	0	0

Step-3:T flip-flop – If value of Q changes either from 0 to 1 or from 1 to 0 then input for T flip-flop is 1 else input value is 0.

Qt	Qt+1	T
0	0	0
0	1	1
1	0	1
1	1	0

Draw input table of all T flip-flops by using the excitation table of T flip-flop. As nature of T flip-flop is toggle in nature. Here, Q3 as Most significant bit and Q1 as least significant bit.

Input table of Flip-Flops
T3	T2	T1
0	0	1
0	1	0
1	1	1
0	0	1
0	1	0
1	1	1

Step-4:design required circuit using expressions of K-maps:

Ripple Counter

A n-bit ripple counter can count up to 2ⁿ states. It is also known as MOD n counter. It is known as ripple counter because of the way the clock pulse ripples its way through the flip-flops. Some of the features of ripple counter are:

1. It is an asynchronous counter.
2. Different flip-flops are used with a different clock pulse.
3. All the flip-flops are used in toggle mode.
4. Only one flip-flop is applied with an external clock pulse and another flip-flop clock is obtained from the output of the previous flip-flop.
5. The flip-flop applied with external clock pulse act as LSB (Least Significant Bit) in the counting sequence.

A 3-bit Ripple counter using JK flip-flop –

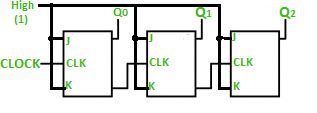
Truth Table –

Counter State	Q2	Q1	Q0
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

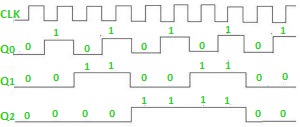
Timing diagram –

Let us assume that the clock is negative edge triggered so above counter will act as an up counter because the clock is negative edge triggered and output is taken from Q.

---

Shift Registers

The information stored within these registers can be transferred with the help of shift registers. Shift Register is a group of flip flops used to store multiple bits of data.

Shift registers are basically of 4 types. These are:

1. Serial In Serial Out shift register
2. Serial In parallel Out shift register
3. Parallel In Serial Out shift register
4. Parallel In parallel Out shift register

Serial-In Parallel-Out shift Register (SIPO) –

the register is loaded with serial data, one bit at a time, with the stored data being available at the output in parallel form.

Serial-in to Serial-out (SISO) -

the data is shifted serially “IN” and “OUT” of the register, one bit at a time in either a left or right direction under clock control.

Parallel-In Serial-Out Shift Register (PISO) –

the parallel data is loaded into the register simultaneously and is shifted out of the register serially one bit at a time under clock control.

Parallel-In Parallel-Out Shift Register (PIPO) –

the parallel data is loaded simultaneously into the register, and transferred together to their respective outputs by the same clock pulse.

Applications of shift Registers –

• The shift registers are used for temporary data storage.
• The shift registers are also used for data transfer and data manipulation.
• The serial-in serial-out and parallel-in parallel-out shift registers are used to produce time delay to digital circuits.
• A Parallel in Serial out shift register us used to convert parallel data to serial data.