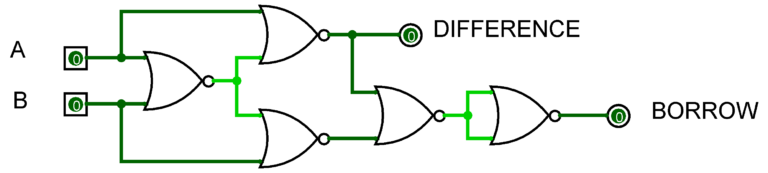
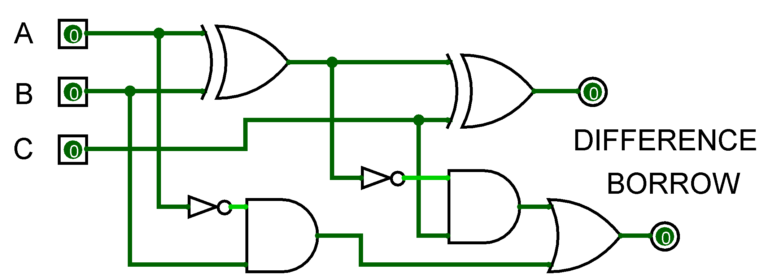
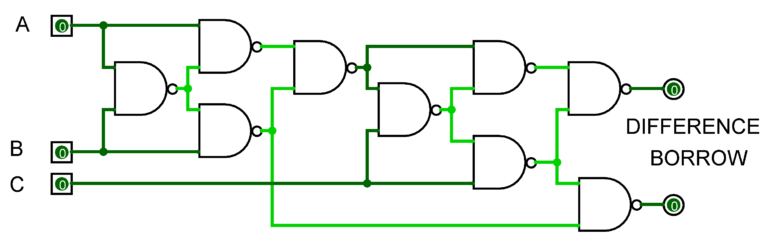
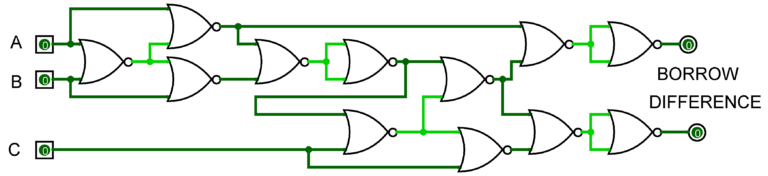
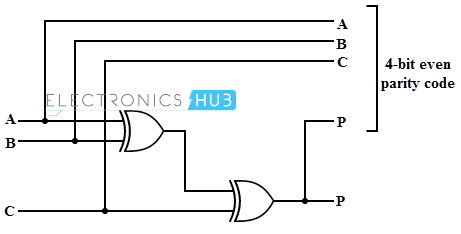
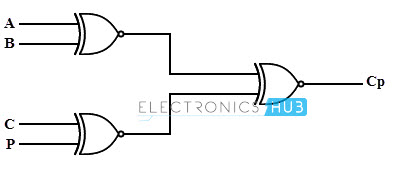
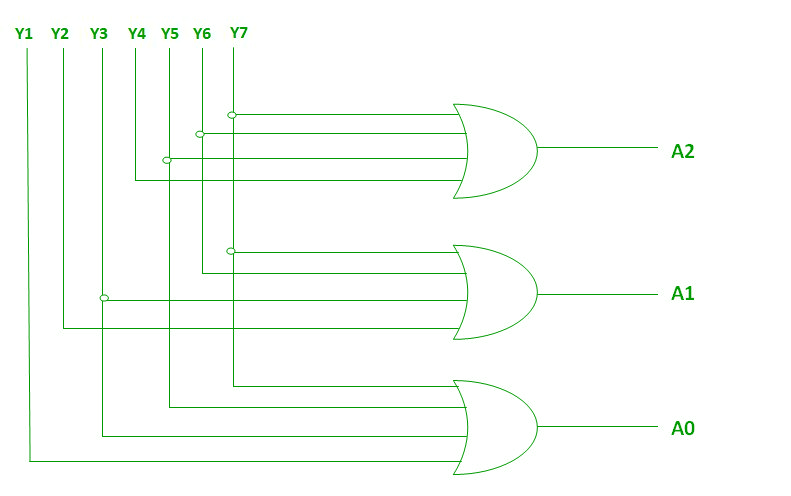
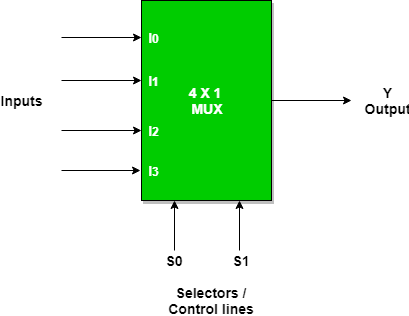
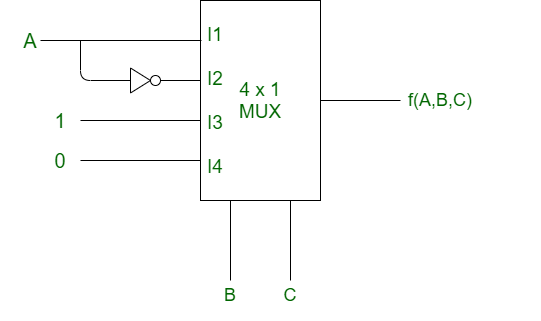
Combinational circuit design
Procedure –
- Identify the number of inputs and outputs of the circuit..
- Creating the Truth Table.
- Simplify the Boolean function for each output.
- Constructing circuit using Boolean function obtained from third step.
Example -
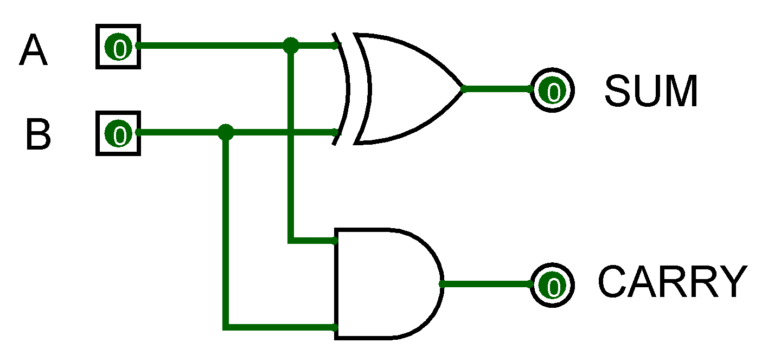
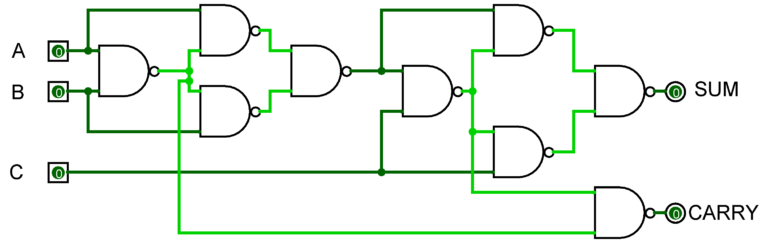
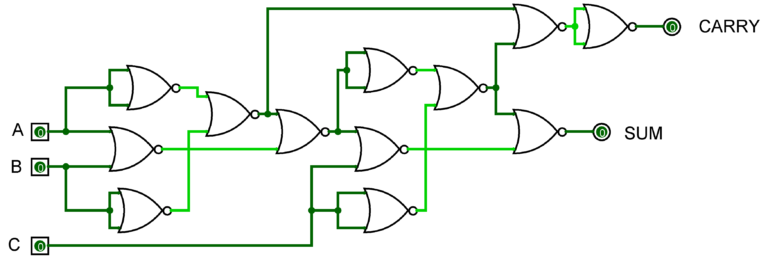
Q) we have to create a circuit that can add two bits.
Step 1: we require two inputs (A, B) and two outputs one for sum (S) of two bits and another for carry (C).
Step 2:
| AB | Sum | Carry |
|---|---|---|
| 00 | 0 | 1 |
| 01 | 1 | 0 |
| 10 | 1 | 0 |
| 11 | 0 | 1 |
Step 3:
For Sum,
Sum = A'B + AB' = A XOR B
For Carry,
Carry = AB = A AND B
Step 4: